Quantum Fundamentals: Winter-2026
Extra practice (SOLUTION): Due W5 D5
- Dimensional Analysis of Kets
S1 5489S
\(\left\langle {\Psi}\middle|{\Psi}\right\rangle =1\) Identify and discuss the dimensions of \(\left|{\Psi}\right\rangle \).
Taking the Hermitian adjoint of a ket does not change the dimensions/units of the ket, so since the bracket is dimensionless, the ket \(\left|{\psi}\right\rangle \) is also dimensionless.
For a spin-\(\frac{1}{2}\) system, \(\left\langle {\Psi}\middle|{+}\right\rangle \left\langle {+}\middle|{\Psi}\right\rangle + \left\langle {\Psi}\middle|{-}\right\rangle \left\langle {-}\middle|{\Psi}\right\rangle =1\). Identify and discuss the dimensions of \(\left|{+}\right\rangle \) and \(\left|{-}\right\rangle \).
Similar to the previous part, each term of the left hand side must be dimensionless. Therefore, the spin states \(\left|{+}\right\rangle \), and \(\left|{-}\right\rangle \) are both dimensionless.
In the position basis \(\int \left\langle {\Psi}\middle|{x}\right\rangle \left\langle {x}\middle|{\Psi}\right\rangle dx = 1\). Identify and discuss the dimesions of \(\left|{x}\right\rangle \).
Here, the integral is dimensionless, but the \(dx\) introduces dimensions of length. We already know the \(\left|{\Psi}\right\rangle \) is dimensionless, so \(\left|{x}\right\rangle \) must have dimensions of inverse square root length, \(1/\sqrt{L}\).
\[\int \left\langle {\Psi}\right|\underbrace{\left|{x}\right\rangle }_{(\frac{1}{\sqrt{L}})}\underbrace{\left\langle {x}\right|}_{(\frac{1}{\sqrt{L}})}\left|{\Psi}\right\rangle \underbrace{dx}_{L} = 1\]
- ISW Right Quarter
S1 5489S
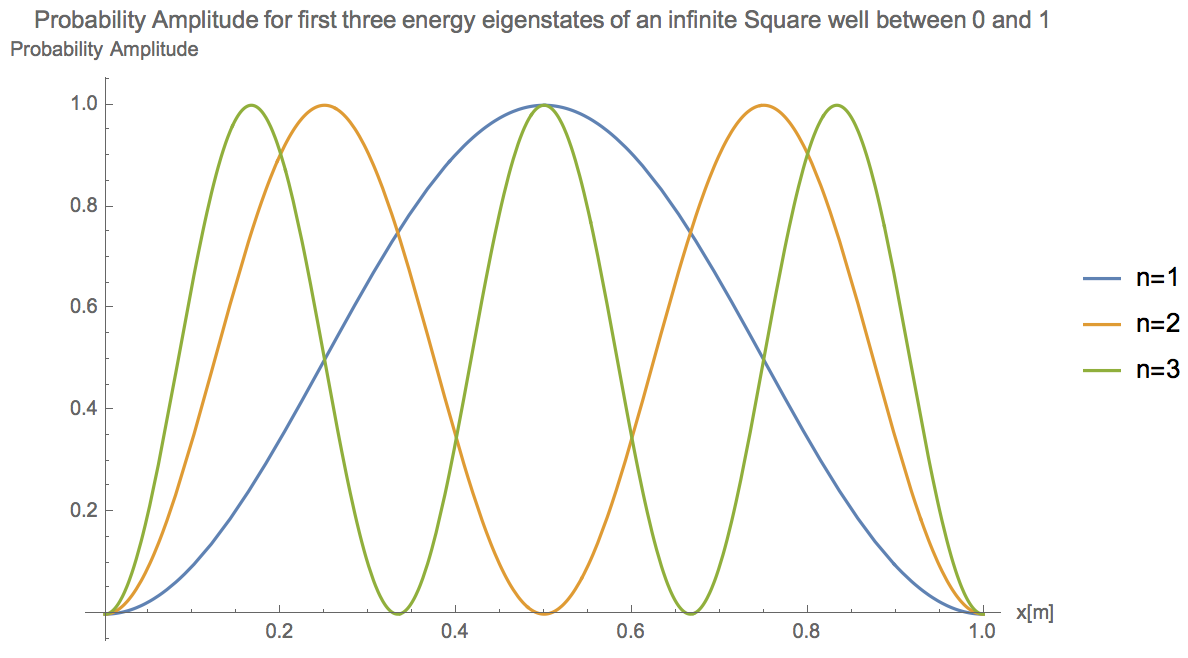
A particle is confined in a one-dimensional infinite square well on \(0<x<L\). For each of the first three energy eigenstates (i.e., \(n=1,2,3\)), calculate the probability that a position measurement yields a result in the region \(\frac{3L}{4}<x<L\).
The probability of finding the particle in a region between \(x\) and \(dx\) is \(|\psi|^2dx\). To add up these probabilities, I integrate the relevant energy eigenstate over the region of interest: \begin{eqnarray*} \mathcal{P}(3L/4<x<L) &=& \int_{3L/4}^{L} |\varphi_n(x)|^2 dx\\ &=& \int_{3L/4}^{L} \frac{2}{L} \sin^2 \left( \frac{n\pi x}{L} \right) dx\\ &=& \int_{3L/4}^{L} \frac{2}{2L} \left[1-\cos \left( \frac{2n\pi x}{L} \right)\right] dx\\ &=& \left. \frac{1}{L} \left[x-\frac{L}{2n \pi}\sin \left( \frac{2n\pi x}{L} \right)\right]\right|_{3L/4}^{L}\\ &=& \frac{1}{L} \left[\left(L-\frac{3L}{4}\right)-\left(\frac{L}{2n \pi}\sin \left( \frac{2n\pi L}{L} \right) - \frac{L}{2n \pi}\sin \left( \frac{2n\pi 3L/4}{L} \right) \right)\right]\\ &=& \left[\frac{1}{4} + \frac{1}{2n \pi}\sin \left( \frac{3n\pi}{2} \right)\right]\\ \end{eqnarray*}
For the first three energy levels: \begin{eqnarray*} \mathcal{P}(3L/4<x<L, n=1) &=& \left[\frac{1}{4} + \frac{1}{2\pi}\sin \left( \frac{3\pi}{2} \right)\right]\\ &=& \frac{1}{4} - \frac{1}{2\pi} \\ &\approx& 0.09\\ \mathcal{P}(3L/4<x<L, n=2) &=& \left[\frac{1}{4} + \frac{1}{4\pi}\sin \left({3\pi} \right)\right]\\ &=& \frac{1}{4} \\ \mathcal{P}(3L/4<x<L, n=3) &=& \left[\frac{1}{4} + \frac{1}{6\pi}\sin \left( \frac{9\pi}{2} \right)\right]\\ &=& \frac{1}{4} + \frac{1}{6\pi} \\ &\approx& 0.30\\ \end{eqnarray*}
I notice that as \(n\) increases, the particle is more likely to be found near the edges of the well, away from the center. When I graph the probability amplitude for the first three eigenstates, these numbers seems reasonable.